NOTA IMPORTANTE - i video vanno scaricati uno per uno, seguendo i collegamenti associati (pazientare per il caricamento). Nelle didascalie qui di seguito, i numeri indicano i minuti e secondi (0':00" ecc.) dall'inizio dei filmati. Non vi sono tracce audio perchè sono stati illustrati a commento diretto.
Si tratta di parte di una videoteca più estesa; il materiale è fruibile ad uso strettamente personale, o didattico e comunque gratuito, citandone gentilmente la provenienza.
I quattro modelli più classici dei moti Planetari
Confronto diretto tra i modelli cinematici più classici per la descrizione dei moti planetari, con particolare riguardo alle loro fasi retrograde ed alle anomalie.
Apollonio di Perga: La Terra è al centro del sistema e ogni pianeta è portato da un epiciclo su un cerchio deferente.
Aristarco di Samo: Il Sole è al centro del sistema e le retrogradazioni conseguono alla combinazione dei moti della Terra e di ciascun pianeta, ognuno centrato sul Sole.
Copernico: Il Sole è al centro e i pianeti, tranne la Terra, sono portati da un doppio epiciclo su un deferente quasi centrato sul Sole.
Keplero: Tutti i pianeti sono in orbite ellittiche col Sole in uno dei fuochi. Vengono così meglio approssimate le anomalie di eccentricità.
NOTA - I nomi citati non escludono altri studiosi che si ritiene abbiano contribuito indipendentemente all'introduzione delle idee illustrate, in qualche caso anticipandole.
Eccentrici, equanti ed ellissi.
00 - L'ipotesi più semplice per un moto orbitale: una traiettoria circolare uniforme, con la Terra al centro, e dalla quale un satellite si vede percorrere angoli uguali in tempi uguali (lancetta di orologio).
00:21 - Seconda possibilità: moto come il precedente, ma non centrato sulla Terra, che così non è più il punto equante (differenza tra un corpo visto in moto angolare uniforme dalla Terra e dal centro di movimento).
00:50 - Terza combinazione: il punto equante non coincide nè con la Terra, nè col centro geometrico dell'orbita, ma allineato con questi.
Si produce una anomalia più marcata che nel caso precedente; cambiano sia la distanza dalla Terra, sia la velocità lungo la traiettoria.
1:32 - Orbita ellittica con la Terra in un fuoco: non vi è più alcun punto dal quale si possa osservare un moto angolare uniforme.
1:56 - Il raggio vettore Terra-satellite copre aree uguali in tempi uguali (seconda legge di Keplero).
2:06 - Uguale proprietà vale per un moto rettilineo uniforme, in tal caso visto da qualsiasi punto: i triangoli così descritti hanno la stessa base e la stessa altezza.
Moti orbitali a velocità variabile: le soluzioni dei Caldei.
Prima dello sviluppo dei modelli greco-ellenistici, Nabu-rimanni (VI sec. A.C.) e Kidinnu (IV sec.) studiarono le anomalie lunari e planetarie approssimandole matematicamente. Nabu-rimanni enunciò una regola discontinua a gradini (sistema "A", in rosso), a due o tre velocità distinte nel corso dello zodiaco. Kidinnu elaborò una regola di variazione continua a dente di sega o "zig-zag" (sistema "B", in blu), che si accorda molto meglio con l'osservazione. Nel diagramma, in ordinate è la velocità angolare e in ascissa il periodo (x2). In verde, per confronto, è un corpo in moto circolare uniforme (C); in grigio un corpo in moto kepleriano (K), a variazione pseudo-sinusoidale.
Molti secoli prima prima di Keplero, le funzioni A e B dei caldei-seleucidi rappresentano le uniche teorie conosciute di moti celesti a velocità intrinsecamente variabile, a fronte di una moltitudine di modelli successivi costruiti sempre su combinazioni additive di moti circolari uniformi, sia in caso geocentrico che eliocentrico.

Tempo e misura della longitudine.
0:0 - Veduta della Terra dal Polo Nord, col meridiano zero in alto.
Un orologio segna il tempo solare nella località a, su un quadrante a 24 ore (freccia gialla = Sole).
0:06 - Spostandosi verso ovest gli orologi locali indicano orari in anticipo: potendo viaggiare a mezzogiorno alla velocità della rotazione diurna, si raggiungerebbero i successivi luoghi B, C e D sempre a mezzogiorno.
0:20 - Si parte ora da A trasportando un orologio regolato qui verso B; durante il viaggio questo continua a segnare l'ora di A. Al polo si vede crescere l'angolo di longitudine corrispondente al tragitto.
0:34 - Arrivati in B, si osserva la differenza fra l'ora locale di B e quella importata da A.
Su un quadrante di 24 ore, l'angolo fra le lancette orarie è uguale all'angolo di longitudine fra le due località. Per ogni 15 gradi di longitudine la differenza di tempo è un'ora: in diminuzione verso ovest, in aumento verso est.
Il moto conico precessionale è conseguenza delle forze lunisolari esercitate sul rigonfiamento equatoriale della Terra, che tendono a diminuirne l'inclinazione orbitale.
0:0 - La Terra è schematicamente al centro del firmamento; si riportano il piano e la traccia dell'eclittica (in rosso).
0:15 - Coordinate geografiche, asse di rotazione diurna e inizio della sua deriva.
0:30 - Il movimento descrive un doppio cono nord-sud con apertura pari al doppio dell'inclinazione.
0:35 - L'inclinazione (all'incirca costante) è riportata anche fra eclittica ed equatore celeste (bianco).
0:45 - Compaiono l'intersezione eclittica-equatore (punti equinoziali) e la griglia delle coordinate celesti, definite su questi stessi elementi.
1:00 - I mesi del calendario e i segni zodiacali vengono definiti e mantenuti coerentemente col ciclo annuo e l'insieme delle coordinate celesti: l'intero complesso appare in movimento parallelamente al piano dell'eclittica.
1:25 - Si evidenzia la fissità delle costellazioni (sono elencate quelle zodiacali), e la mancata corrispondenza dei segni associati tradizionalmente ad esse.
Ai poli celesti corrispondo parimenti posizioni diverse nel corso del ciclo, secondo traiettorie centrate sui poli eclitticali.
Cosmologia della Divina Commedia
Nella Commedia Dante Alighieri rappresenta in forma moderna la struttura cosmologica di tradizione aristotelica, nella quale il centro della Terra è il centro di gravità dell'Universo, in qualità di suo punto più basso. Allontanandosene, si attraversa la gerarchia delle sfere elementari, poi planetarie e quindi celesti, nel classico ordine concentrico. Proseguendo nell'Empireo, la sua descrizione diviene invece più astratta, e non più riconducibile ad uno spazio euclideo familiare.
Keplero: Harmonices Mundi (la "Musica delle Sfere").
In questo suo lavoro Keplero ricercò un possibile rapporto fra velocità angolari dei pianeti e le note musicali, riscalate opportunamente a ottave udibili. Si avvertirà l'ampia variazione corrispondente alla sensibile ellitticità dell'orbita di Mercurio, e quella inavvertibile di Venere, a raggio e velocità orbitale pressochè costante.
Il progetto è di Anna Lonbardi, l'esecuzione di Arcangelo Di Donato (diritti degli autori).
Riferimenti:
Anna Lombardi:
Docente di Storia della Scienza, ha lavorato per le Università di Milano e di Padova, e in progetti fra arte e scienza.
Arcangelo Di Donato:
Architetto, si occupa di design e di progetto in senso ampio fino ad
includere l'elaborazione musicale.
L’ordine planetario nelle ore e nella settimana.
0:00 - I sette “pianeti” vengono ordinati dal più lontano al più vicino alla Terra (Saturno, Giove, Marte, Sole, Venere, Mercurio, Luna).
0:07 – Questo ordine di distanza (D) è manifestato inversamente dall’ordine delle velocità massime dei moti propri (V).
0:17 – Ciascuna delle 24 ore rappresenta un pianeta, secondo il medesimo ordine, iniziando come esempio dalle ore zero.
0:29 – La serie si ripete, sempre dal più lento al più rapido, ma chiudendosi sfasata.
0:40 – Procedendo da un giorno all’altro, alla stessa ora corrisponde un pianeta senza la medesima continuità con quello del giorno prima.
1:28 – Dopo 7 giorni (168 ore) la sequenza si ripete secondo l’ordine Saturno, Sole, Luna, Marte, Mercurio, Giove Venere; a questa corrisponde la serie dei giorni settimanali.
1:38 – I pianeti vengono riordinati in un ciclo di sette, di nuovo nell’ordine discendente di prima .
2:06 – I due ordini sono ancora in rapporto secondo una alternanza di opposti: saltando di giorno in giorno al terzo successivo, dalla successione distanza/velocità si ritorna a quella settimanale.
Se la Terra si muove in un anno attorno al Sole, e le stelle non sono tutte equidistanti, di tutto questo dev'essere possibile una verifica.
0:30 - Si osserva una stella presumibilmente vicina: compare la linea di mira Terra-stella, e se la prima si muove, la posizione della seconda sembrerà cambiare nel corso dei mesi. In lontananza compaiono la posizione media (crocetta) e il tragitto apparente, che rispecchia il cammino della Terra.
0:45 - Altra ipotesi ammissibile, quella di poter semplificare lo scenario ammettendo che le altre stelle si collochino su una sfera arbitrariamente grande, con funzione di sfondo.
0:52 - Si costruisce un triangolo Terra-Sole-stella e si evidenzia l'angolo al vertice stellare.
Più l'astro osservato è distante, più il suo movimento sullo sfondo del firmamento risulta piccolo.
1:00 - Ugualmente più piccolo è il valore di tale angolo, noto come parallasse annua (pi greco). La realtà di questo effetto è una prova del moto annuo terrestre e la sua misura (Bessel, 1838) è l'unica tecnica strumentale diretta per la stima delle distanze stellari.
Assumendo come unità la distanza Terra-Sole (Unità Astronomica), l'angolo in questione permette di risolvere geometricamente l'altezza D.
NOTA - i minimi valori reali di D sono superiori all'unità astronomica di 5 o 6 ordini di grandezza, quindi altezza e ipotenusa si considerano equivalenti, così come la base ad un arco; nella formula Pi è espresso in radianti.
Molte stelle, anche se al telescopio appaiono uniche, sono in realtà sistemi binari o multipli. Viene presentato il caso, abbastanza tipico, di una coppia orbitante costituita da due astri di temperatura e luminosità diverse.
0:0 - Se il piano orbitale del sistema si presenta abbastanza inclinato, la sua natura passa inosservata e la luminosità di insieme appare costante nel tempo.
0:10 – Diminuzione dell’inclinazione visuale.
0:15 – Al di sotto di un certo angolo, le stelle iniziano ad occultarsi a vicenda, cosicchè la luminosità totale (Mv = Magnitudine apparente) subisce dei cali periodici.
0:25 - Il minimo principale della curva di luce corrisponde all'occultamento dell'astro più luminoso, in questo caso il più piccolo e caldo. La curva di luce presenta la situazione reale della binaria Beta Persei, la cui variabilità è riconoscibile visualmente e già nota agli arabi antichi.
0:45 - Nel caso di un piano orbitale meno inclinato, le eclissi possono essere totali: i minimi sono più profondi e mantenuti per tutto il tempo di transito, perciò presentano un fondo piatto.
1:00 - Geometrie più complesse danno luogo a curve di luce più peculiari. Le stelle possono essere schiacciate per la rotazione, inviluppate in corone estese, con scambio parziale di gas tra le componenti, o interessate da campi magnetici rilevanti. Tale sembra il caso di Beta Lyrae.
Alla variazione totale di luminosità si possono accompagnano diversi mutamenti spettrali periodici, come quello ben noto dovuto al fatto che la luce della componente più brillante viene riflessa sull'astro più debole, con effetto analogo a quello delle fasi lunari.
1:32 - L'analisi della curva di luce permette di dedurre molte di tali caratteristiche anche senza che gli strumenti ottici riescano a risolvere le singole stelle.
Il ciclo diurno secondo la stagione e la latitudine.
Sono illustrate le traiettorie del Sole in corrispondenza delle sue posizioni solstiziali ed equinoziali.
0:00 -0: 17 - Tracciamento dell'eclittica con la sua inclinazione.
0:30 - L'orizzonte seziona la sfera celeste, si riportano le massime, minime e intermedie declinazioni del Sole, e gli archi di visibiltà a 45 gradi di latitudine N.
0:45 - Spostamento al tropico del Cancro: la latitudine è pari all'inclinazione dell'eclittica e al solstizio estivo il Sole culmina allo zenith senza gettare ombra.
1:05 - Spostamento all'equatore: Il Sole rimane sull'orizzonte per metà del ciclo diurno, indipendentemente dalla stagione. L'illuminazione è permanentemente equinoziale.
1:25 - Spostamento al circolo polare artico: al solstizio invernale il Sole rasenta l'orizzonte S e non sorge (se non per effetto di rifrazione). Al solstizio estivo rimane visibile anche a mezzanotte.
1:40 - Spostamento al polo N: il sorgere e tramontare del Sole non è dovuto al moto diurno ma a quello annuo. Il Sole compare lentamente all'equinozio di giugno e rimane visibile continuativamente per 6 mesi; tramonta all'equinozio di settembre lasciando posto a una notte polare di altri 6. Il computo delle ore qui non può che essere vincolato arbitrariamente ad un meridiano di riferimento.
La Luna come satellite del Sole e della Terra.
Ovvero: come gli schemi troppo semplificati possono risultare fuorvianti.
0:00 - Si inizia con una classica rappresentazione della traiettoria lunare, necessariamente fuori scala (qui di un fattore 100).
0:30 - L'orbita lunare attorno alla Terra viene progressivamente riportata in scala di distanza (380mila km. dalla Terra e 150 milioni dal Sole).
0:48 - L'orbita lunare è ora ridotta a un fattore 50 e la traccia epicicloidale comincia a spianarsi; rimane disegnata l'orbita d'inizio per riferimento.
1:10 - Le distanze sono ora in scala 1:1: nel quadro d'insieme si vede come la traiettoria della Luna non rivolga mai alcuna convessità verso il Sole (ciò che difficilmente si può rappresentare nei disegni statici).
1:35 - Eliminando la Terra, la Luna proseguirebbe il suo moto come satellite del Sole, che è l'astro predominante: la velocità orbitale geocentrica della Luna è di un ordine di grandezza inferiore a quella eliocentrica.
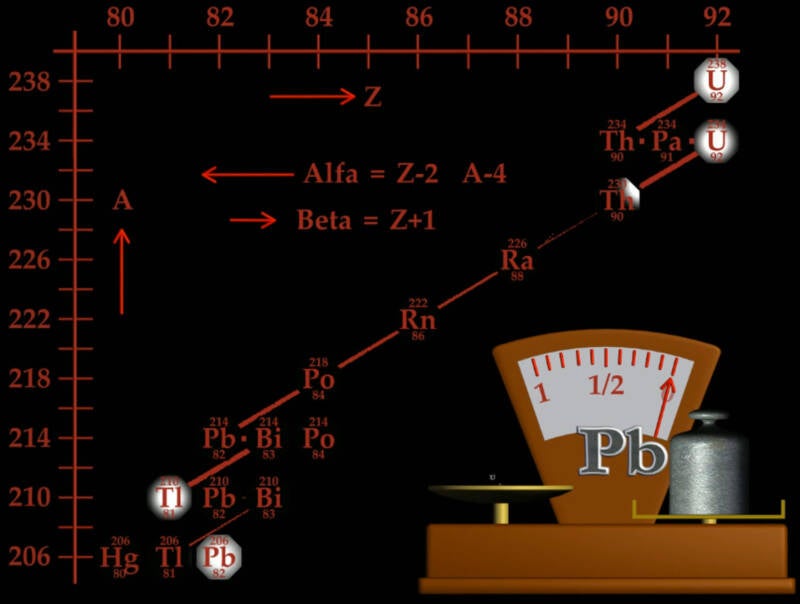
Decadimento radioattivo e radiodatazione
In ascissa è il numero atomico Z (protoni) e in ordinata il numero di massa A (protoni e neutroni). Si parte con una quantità data di un radiosiotopo per finire con un nucleo stabile; questo è l’esempio dell’Uranio-Piombo.
0:07 – Sono elencati i nuclidi che costituiscono la catena tipica di decadimento, che consiste in emissione spontanea di particelle alfa (nuclei d’elio), o beta (trasmutazione di un neutrone in un protone). Nel primo caso il nucleo perde due cariche, scalando a sinistra di due posizioni e perdendo quattro unità di massa; nel secondo acquisisce invece una carica e il numero atomico risale a destra di uno, perdendo un elettrone nucleare ma conservando il numero di massa.
0:23 – All’analisi, la metà dell’uranio è ora trasformata in un isotopo stabile del piombo: questo è il tempo di dimezzamento. Il decadimento è esponenziale e un'analisi differenziale permette, in linea di principio, di determinare l’età del campione originario.
NOTA - Ogni prodotto succedaneo ha a sua volta un tempo di decadimento proprio, e talvolta può decadere facoltativamente, con diverse probabilità, tanto con emissione alfa che beta. Il nucleo stabile finale, in questo esempio, è univoco. Non si considerano qui gli eventi meno probabili di fissioni spontanee, nè di altre emissioni (gamma, neutrini) associate a specifici decadimenti, ma indifferenti per le proprietà dei nuclei.
La sintesi additiva e sottrattiva dei colori
La luce bianca visuale può essere composta mediante la sintesi di tre colori base: Rosso, Verde, Blu, coi quali l'occhio umano valuta la tonalità risultante.
0:04 - Si isolano le tre componenti spettrali che appaiono visualmente come R, V e B.
0:16 - La somma Blu+Verde dà il colore Ciano (C), Blu+Rosso il Magenta (M), Verde+Rosso il Giallo (G). I tre B+V+R ricompongono lo spettro intero (bianco).
0:25 - Si riproducono quindi il Ciano come parte dello spettro che non comprende il Rosso, il Magenta come quello che non comprende il Verde, e il Giallo come quello che non comprende il Blu (complementari di R, V e B). R, V e B sono quindi monocromatici, C, M e G derivano invece dall'esclusione selettiva di ognuno di questi dall'intera gamma visibile.
0:40 - La sintesi sottrattiva dei colori si ha filtrando Ciano, Magenta e Giallo, e osservando la tonalità trasmessa; l'occhio umano discrimina il colore in questo modo (la filtrazione completa estingue l'intero spettro: nessuna trasmissione = nero).
L'invarianza della velocità della luce obbliga a rivedere alcuni concetti di base riguardo al tempo (esempio tratto da Einstein).
0•00 - Si prendono due sistemi di riferimento, uno in quiete ed uno in moto rettilineo uniforme. Due osservatori sono in treno e due a terra, collocati reciprocamente alla stessa distanza fissa.
0:30 - Viene accesa una luce a metà carrozza, in una posizione equidistante da tutti gli osservatori, che possono misurarne l'istante di arrivo.
0:38 - Per gli osservatori anteriore (a) e posteriore (p) nella carrozza, il segnale luminoso arriva contemporaneamente (stesso istante negli orologi a bordo).
0:55 - Lo stesso evento non verrebbe rilevato allo stesso modo dagli osservatori a terra: il passeggero posteriore p sta andando incontro alla posizione della sorgente luminosa, quindi dovrebbe vederla per primo.
1:03 - In questo momento la luce giunge a entrambi i due sulla banchina, ma non ancora al passaggero anteriore. I tempi rilevati non possono coincidere.
1:08 - Lo stesso evento che per due osservatori appare contemporaneo, può non esserlo per altri in moto rispetto a quelli.
L'invarianza della velocità della luce era implicita nella teoria elettromagnetica di Maxwell, e fu confermata dall'esperimento di Michelson e Morley. Ha portato infine Einstein ad una completa revisione della nozione di simultaneità, introducendo nuovi concetti e formalismi nella misura di spazio e di tempo.
Sfere omocentriche e modelli storici dei moti Planetari, in transizione visuale.
Scenario classico dei modelli cosmologici più antichi: la Terra è immobile al centro dell’universo.
0:00 – Compaiono la Terra, un pianeta e la cintura dello zodiaco coi 12 segni.
0:10 - Compaiono 2 cerchi imperniati su poli diversi: su quello interno si immagina sia fissato il pianeta.
0:14 - I cerchi ruotano alla stessa velocità e opposte direzioni: il pianeta descrive un andirivieni ciclico secondo una ippopeda sferica. L'ampiezza dell'oscillazione dipende dall'inclinazione dei poli di rotazione dei cerchi; questi costituiscono il cuore del meccanismo di Eudosso e rappresentano gerarchicamente le ultime due sfere del pianeta.
0:30 - Per rendere conto del movimento del pianeta secondo lo zodiaco, i cerchi interni vengono imperniati su un altro di ordine superiore, che ruota sui poli dell'eclittica (gli elementi eclitticali sono in rosso).
0:42 – Vengono introdotte le sfere omocentriche; i cerchi ne sono una semplificazione.
1:10 - Compaiono l'equatore, un meridiano e i poli celesti. Questa è la prima sfera e ad essa compete il moto diurno d’insieme, qui omesso, trascinando con sé l'intero sistema.
1:40 – Transizione al modello epiciclico, basato sull’idea di Apollonio di Perga, e successivamente elaborato da Ipparco e Tolomeo. Il pianeta si muove su un cerchio ausiliario, mosso a sua volta su un cerchio primario (il deferente) attorno alla Terra.
Il pianeta reale non retrograda, ma visto dalla Terra (linea di mira in rosso) sembra intercalare inversioni di moto periodiche sullo sfondo zodiacale. Ora si rende possibile una spiegazione della sua diversa luminosità, essendo variabile la distanza.
2:20 – Transizione al modello eliocentrico: scompare l’epiciclo e appare l’orbita della Terra. Mente la Terra viaggia intorno al Sole, la linea di mira oscilla in modo analogo.
Anche qui il pianeta non retrograda, ma sembra invertire il movimento rispetto allo sfondo stellato, e si può render conto ugualmente bene della variazione di distanza – luminosità. Ma oltre a ciò, ora le fasi retrograde sono necessariamente correlate all’opposizione al Sole: questo non era implicito nei modelli precedenti.
NOTA – il video riproduce i meccanismi di base senza considerare tutti i dettagli, gli sviluppi e le varianti di ciascun modello.
Il sistema originario di Eudosso era costituito da 27 sfere; nella revisione di Callippo da 34 e in quella di Aristotele da 56.
Gravitazione in una massa sferica.
0:00 - La Terra viene vista in sezione, e si immagina un tunnel libero attraverso il diametro.
0:09 - Un oggetto è lasciato libero di cadere ad una estremità. In rosso viene indicata la forza di gravità e in grigio la velocità: la prima decresce avvicinandosi al centro (punto abarico), la seconda aumenta fino al centro per diminuire fino a zero all'estremità opposta.
0:16 - Compaiono due scale con lo stesso codice di colore, con indicazione del valore assunto dalle due grandezze.
0:40 - Si apre una cavità interna; la massa del pianeta diminuisce ed è ora confinata su un guscio. Entro questa cavità la forza gravitazionale è nulla e il moto è impresso al grave esclusivamente entro lo spessore del guscio.
I valori di velocità e accelerazione gravitazionale sono ora inferiori, ma soprattutto l'andamento è diverso: la loro variazione si manifesta soltanto entro il mantello e non nella cavità. Qui il moto è inerziale, e quindi uniforme.
0:57 - All'esterno di un guscio sferico (intero) il campo gravitazionale è simile a quello di una sfera piena, e soltanto inferiore in intensità. In assenza di attriti un satellite vi può orbitare come attorno ad un corpo pieno.
1:01 - Nella cavità un corpo può rimanere in quiete in qualunque posizione.
1:04 - Più corpi, in teoria, potrebbero muoversi in un sistema orbitale, in condizioni dinamiche simili a quelle che si verificherebbero nello spazio e senza alcuna interferenza dallo strato materiale circostante.
Eclissi lunisolari: regole generali.
0:00 – Sole, Terra stazionaria e Luna in orbita. All'inizio viene presentato un assetto semplificato dei moti, senza riprodurne i reali parametri orbitali.
0:08 – Luna piena in ombra alla Terra.
0:16 – Luna nuova in transito e congiungente Terra-Sole: caso ideale di una eclisse pienamente centrata.
0:21 – Eclisse di Luna: il globo rimane leggermente illuminato dall'atmosfera terrestre, e nascosto al Sole fino ad un paio d'ore.
0:23 – Si considera il moto orbitale del sistema intorno al Sole.
0:29 – Allineamento (eclisse di Sole).
0:32 - Allineamento (eclisse di Luna).
0:37 - Allineamento (eclisse di Sole).
0:41 – Vengono progressivamente introdotte le altre caratteristiche dei moti orbitali. Qui compare il piano dell'orbita terrestre (scuro e incorniciato in rosso).
0:43 – Viene riprodotta l'inclinazione della traiettoria lunare (5 gradi circa, qui molto accentuati).
0:50 – La Luna incontra il piano dell'eclittica due volte ad ogni ciclo: compare la linea dei nodi (ascendente = omega; discendente = omega rovescio).
Ora non si verificano eclissi perchè la Luna nuova e piena sono scostate dalla direttrice Terra-Sole.
Spostamento del sistema di alcuni mesi.
1:07 – Le circostanze di allineamento presuppongono ora una seconda condizione: oltre alla fase nuova o piena, anche il fatto che le stesse abbiano luogo laddove la linea dei nodi è orientata al Sole.
Ripresa del moto di rivoluzione annua del sistema.
1:24 – Altra condizione di allineamento, dalla parte opposta alla prima: qui ancora il plenilunio e il novilunio comportano eclissi.
1:28 - Ripresa del moto di rivoluzione annua del sistema. In questo quadro le eclissi possono verificarsi in due determinati periodi dell'anno, opposti di sei mesi: sono indicati dalla medesima linea dei nodi, riportata in grande e fissa sull'eclittica.
2:00 – Sosta e comparsa del moto di nutazione. Indipendentemente dalla traslazione del sistema Terra-Luna, il piano dell'orbita lunare ruota, e con esso la sua intersezione e i nodi.
2:30 – Compare un quadrante per il ciclo di nutazione, che si compie in circa 18,6 anni.
2:40 – Questo ciclo temporale viene riportato all'orologio del moto annuo coi 12 mesi.
Ripresa del moto annuo, ora con scalatura proporzionale dei periodi orbitali e di nutazione.
2:48 – Ricompare la linea dei nodi ricondotta al centro, come una lancetta che indica i luoghi e i tempi delle possibili eclissi.
3:08 – I fenomeni si concentrano ancora in due periodi all'incirca opposti, ma in progressivo spostamento nel corso dei mesi, via via a precedere di anno in anno.
Viene omessa l'orbita lunare, irrilevante a questa scala, e le fasi lunari vengono riprodotte in posizione geocentrica.
3:26 – Le eclissi si ripetono a gruppi di due o tre eventi per volta, frequentemente di tipo parziale, qui non differenziato. Nell'arco di qualche anno è evidente la migrazione delle epoche in cui si possono verificare.
Principi di calendario astronomico: il sorgere eliaco di Sirio
Si rappresenta il percorso zodiacale apparente del Sole, nel corso dei 12 mesi.
0:25 - L'orizzonte terrestre, esteso alla sfera celeste, la divide in due. Viene avviata la rotazione diurna della volta celeste, con quadrante delle ore dì/notte, guardando verso oriente.
0:38 - Ci si sofferma all'alba, identificando le ultime stelle visibili al crepuscolo: esse daranno un'indicazione della posizione del Sole in relazione allle stelle che nasconde.
0:50 - Ripetendo l'osservazione a distanza di diversi giorni, all'alba le stesse stelle risultano anticipare la levata (circa 4 minuti al dì), lasciandone vedere altre che precedentemente erano nascoste dal Sole. Qesta è l'osservazione chiave che permette una misura dello spostamento del Sole nello zodiaco.
1:05 - Il sorgere eliaco di Sirio è un esempio particolarmente rappresentativo di istituzione astronomica del calendario. Tenendo conto dell'effetto precessionale, la sua apparizione mattutina segnava l'inizio dell'anno egizio antico (il primo giorno di Thot) e con questo la stagione delle piene estive del Nilo.
Analoghi avvistamenti, all'alba o al tramonto, erano comunemente usati come indicazioni di calendario nelle culture di tutti i tempi e luoghi storicamente conosciuti.
0:00 - Costruzione di un diagramma 3D con lo spettro della radiazione elettromagnetica secondo l'asse X (la lunghezza d'onda aumenta verso dx, la frequenza aumenta verso sx), la temperatura dell'oggetto emittente secondo l'asse Y (in aumento verso il fondo), e l'intensità relativa dell'emissione secondo l'asse Z (in aumento verso l'alto).
0:02 - compare la curva di emissione di corpo nero: essa si sposta al crescere della temperatura (verso il fondo) sviluppando il profilo della caratteristica planckiana.
Vengono mostrate alcune curve caratteristiche di corpo nero; per temperature ambiente o molto basse il massimo dell'emissione è spostato nell'infrarosso (Mc = microonde, Ir = infrarosso, Vs = visibile, Uv = ultravioletto). Le temperature sono indicate in gradi Celsius.
20:00 - Compare il profilo della lunghezza d'onda di picco dell'emissione, con la relazione di Wien della lunghezza d'onda (in micron) in funzione della temperatura (in gradi Kelvin).
00 - Un pendolo oscilla sospeso sul Polo Nord su una Terra in quiete.
00:10 - La Terra ruota, e con essa la direzione di partenza (linea gialla). La direzione di oscillazione del pendolo si mantiene orientata con le stelle.
00:21 - Compaiono le forze di Coriolis ad ogni oscillazione; queste nel complesso agiscono come una coppia di rotazione costante.
00:27 - Disegno della traiettoria del pendolo nel sistema di riferimento della Terra. In questo sistema la direzione e il piano di oscillazione al Polo Nord appaiono ruotare con la velocità del moto diurno.
00:39 - Spostamento a latitudine intermedia. Le deviazioni di Coriolis hanno un andamento più complesso; la rotazione è più lenta (periodo diurno per il seno della latitudine).
1:10 - Spostamento all'equatore. Per la componente in senso meridiano del moto, il verso delle deviazioni di Coriolis si compensa e non vi è rotazione del complesso.
1:20 - Per una oscillazione in senso equatoriale non agisce alcuna deviazione.
All'equatore il pendolo non viene deviato in nessun caso: nel primo si mantiene la direzione (polare), nel secondo il piano di oscillazione (equatoriale).

Classe di stelle variabili intrinseche per pulsazioni.
0:0 - L'astro osclilla attorno ad un valore medio di raggio, densità e temperatura.
0:05 - Compare il grafico della luminosità (magnitudine apparente) in funzione del tempo, con l'andamento tipicamente sinusoidale ma asimmetrico.
0:16 - In modo analogo variano altri parametri fisici quali la temperatura (a dx.). Il caso del diagramma è quello di Delta Cephei, capostipite della categoria (le variazioni di dimensione sono state esagerate per chiarezza).
0:40 - Si danno casi di variabilità analoga per stelle di grandezze fisiche molto diverse: qui aumentano tutte, la curva si alza e si estende, poichè aumenta il periodo.
0:42 - Compaiono una ordinata ed una ascissa in moto per indicare l'aumento rispettivamente del periodo e della luminosità al suo valore medio, stavolta indicata in valore assoluto.
1:05 - Si costruisce il diagramma periodo-luminosità e compare una popolazione di stelle che non si disperde a caso: quelle a oscillazione più veloce sono più piccole e meno luminose, secondo una relazione caratteristica (casi fittizi).
1:12 - Relazione numerica fra magnitudine assoluta (M) e periodo (P) per le Cefeidi. Si differenziano poi due sottocategorie (popolazione I e II) per entrambe le quali vale una precisa relazione periodo-luminosità, ma con parametri di luminosità media significativamente diversi.
Dal geocentrismo all'eliocentrismo: l'indizio dei pianeti interni.
Veduta panoramica dei moti planetari epicicici (semplificati) a partire dall’esterno del sistema solare: Saturno, Giove e Marte su epiciclo e deferente, fino a evidenziare il Sole, i pianeti inferiori (Venere e Mercurio) e la Luna; il tutto in moto geocentrico.
0:42 - Una linea rossa traguarda la Terra, il Sole e gli epicicli di Mercurio e Venere: questi ultimi appaiono sempre allineati col Sole, compiendo un moto annuo sul deferente esattamente come il Sole.
0:52 - Avvicinamento e atterraggio. La periodicità di un anno degli epicicli di Venere e Mercurio che li confina attorno al Sole, è condizione implicitamente richiesta da tale osservazione: i pianeti inferiori appaiono elongarsi periodicamente ad est e ovest del Sole, entro limiti e tempi ben noti, e in questa ipotesi transitando sempre in congiunzione inferiore in entrambe le direzioni. Tale vincolo non vale per quelli superiori.
1:24 - Fuga prospettica e visione esterna: gli epicicli dei pianeti interni ora vengono centrati sul Sole, semplificando così il meccanismo.
1:45 - Rientro sulla Terra e confronto col quadro precedente: ora i pianeti inferiori sono confinati come prima, ma transitano in congiunzione superiore nel corso del moto diretto, inferiore in moto retrogrado. Nel primo caso non si può verificare alcun transito sul disco del Sole, nel secondo sì.
2:15 - Illuminazione e fasi di Venere: con l’osservazione galileiana delle fasi e delle dimensioni di Venere, viene confermata l’idea del suo moto eliocentrico.
Il globo del pianeta, impercettibile ad occhio nudo, venne svelato al telescopio, mostrando la fase di maggiore illuminazione in prossimità della massima distanza dalla Terra (congiunzione superiore). Decentrando il Sole non sarebbe invece spiegabile la fase “piena”. Galileo scrisse una nota criptica preliminare, "La dea degli amori imita le figure di Cinzia", intendendo che Venere imita le fasi della Luna, per garantirsi la priorità della scoperta.
Il sistema planetario secondo Tycho Brahe
Tycho propose una soluzione di compromesso per mantenere al centro del sistema la Terra, mettendo invece gli altri pianeti in orbita attorno al Sole.
0:00 - Si parte da traiettorie eliocentriche (orbita della Terra in rosso, velocità e distanze non in scala).
0:20 - Si fissa la Terra al centro e si sposta il Sole, che porta con sè il resto del sistema.
0:30 - Si ritracciano le orbite planetarie nel nuovo sistema di riferimento fissato alla Terra; i pianeti disegnano ciascuno la propria retrogradazione apparente, in un modo qualitativamente simile al caso di un sistema eliocentrico. Le obiezioni a carattere filosofico-religioso venivano così risolte da un cambio di coordinate.
Peso e massa, gravità e accelerazione.
Quadro conforme alle leggi della meccanica classica (non si considerano effetti relativistici).
0:00 - Un oggetto viene posto su un dinamometro sulla Terra, e questo rileva una determinata forza-peso (p).
0:10 - Se la massa del pianeta diminuisce (Mt), altrettanto si verifica per la forza di attrazione e il peso rilevato; l'oggetto non ha alcun peso se libero nello spazio.
0:27 - Lo stesso oggetto viene incapsulato in un razzo, del quale si misurano velocità (v) e accelerazione (a). Con una spinta costante, la forza peso si manifesta ugualmente costante, e la velocità in continuo aumento.
0:38 - Annullando la spinta, rimane costante la velocità e viene a mancare la forza peso.
Nei moti rettilinei uniformi il sistema non è soggetto a forze ed è da considerarsi inerziale, come quando si trovava in quiete nello spazio: nessun esperimento permette di distinguere tra queste due condizioni (principio di equivalenza di Galileo).
Simile identità di condizioni si osserva per i sistemi sottoposti a forze, tanto che si tratti di accelerazione statica dovuta a gravità, quanto accelerazione dinamica per variazione di velocità (principio di equivalenza di Einstein).
Principi di ottica: come si forma un'immagine.
Un oggetto luminoso si può esemplificare come un insieme di punti emettitori, che irradiano in ogni direzione.
0:08 - Dato un piccolo diaframma (foro stenopeico), per ogni punto si rappresenta un singolo raggio di luce che lo attraversa.
0:15 - Ogni raggio, se va a illuminare uno schermo, vi riprodurrà un elemento di immagine dell'oggetto, che risulterà necessariamente rovesciato. Con questo dispositivo si ottengono immagini ottiche visibili e fotografabili, purchè abbastanza luminose.
0:20 - Allargando il diaframma passerà più luce, ma l'immagine proiettata viene sempre più sfocata, perchè per ogni punto dell'emettitore vi transita non un raggio di luce ma un fascio diffuso e non collimato.
0:25 - Una lente positiva provvede a riallineare i raggi luminosi, che tornano a convergere punto per punto a una determinata distanza. Ogni punto dell'immagine ora è riprodotto non attraverso un foro, ma da un'apertura che raccoglie e restituisce tanta più luce quant'è ampia la sua sezione.
0:40 - Nel caso del cannocchiale astronomico, l'oggetto viene considerato all'infinito (qui una stella al centro dell'asse ottico), e il fascio incidente come parallelo.
0:44 - Per l'osservazione visuale, viene aggiunta un'altra ottica in prossimità del piano focale (qui un'altra lente convergente), che restituisce un fascio parallelo abbastanza piccolo da poter entrare nella pupilla dell'osservatore. Verrà rifocalizzato quindi da questo sulla propria retina, con un fattore d'ingrandimento pari al rapporto tra la lunghezza focale dell'obbiettivo e quella dell'oculare.
Fusi orari, Tempo Universale e cambiamento data
Il tempo civile viene calcolato in base alla culminazione solare media al meridiano locale, che definisce il mezzogiorno.
0:19 – Viene definito un meridiano zero, e l’ora misurata qui definisce il Tempo Universale (T.U.). La freccia gialla (direzione del Sole) definisce il mezzogiorno per ogni altro meridiano (Tempo locale).
0:25 – Alla mezzanotte di TU si ha qui il cambiamento data.
0:40 – Riproiezione della mappa terrestre in piano.
1:00 – Ricapitolazione del trascorrere delle ore secondo le diverse longitudini, ogni 30 gradi (2 ore). La freccia gialla indica sempre il TU, ed ora viene aggiunto il passaggio delle date. Ad est della mezzanotte TU la data è quella del giorno seguente.
1:22 – Altro cambio di data al meridiano zero.
1:30 – A mezzogiorno di TU, si ha la stessa data dappertutto. Dopodichè, all’antimeridiano zero scatta l’incremento della data, quindi le ore del giorno seguente trascorrono avanzando ad est su ogni longitudine. Di norma quindi, spostandosi verso est si avanza nel corso delle ore della giornata; oltrepassando l’ antimeridiano zero va però scalato un giorno. Il sistema è stato introdotto nel 1884; l’antimeridiano è anche detto Linea di Cambiamento Data, e cade in un’area del globo scarsamente abitata, con deviazioni locali per convenienza amministrativa.
Da Australopithecus Afarensis ad A. Africanus.
Da Homo Ergaster a Neanderthal.
Il modello planetario di Filolao.
Filolao ha concepito un modello planetario poco noto e menzionato, ma altamente originale, con al centro un fuoco (Hestia) attorno al quale orbitano tutti gli altri corpi celesti.
In particolare la Terra e la Luna avrebbero lo stesso periodo di rotazione e rivoluzione, dunque dalla nostra posizione sulla Terra vedremmo ogni giorno alternarsi il Sole, la Luna e le stelle, osservando il progressivo procedere degli astri erranti nello zodiaco.
Da nessun luogo della Terra si potrebbe comunque osservare il fuoco centrale, a causa dell'interposizione sincrona di una invisibile Antiterra (A: Antichton) tra essi.
Ciclicità visiva del calendario Maya.
Vengono presentati i cicli di base del calendario tradizionale Maya e i suoi svariati multipli, che nel suo insieme non ha riscontro nel computo delle civiltà mediterranee. La struttura di base era la combinazione di unità di 13 e 20 giorni (lo "Tzolkin") per un ciclo di 260, ma erano ugualmente considerati un periodo di 360, nonchè di molto più lunghi, di significato eminentemente mitologico.
Tempo solare e tempo siderale.
00 - Moto di rotazione della Terra e misura del tempo riferita al ciclo diurno: il tempo civile è sincronizzato ai transiti del Sole su un meridiano dato (tempo solare medio); la divisione è in ore.
00:12 - Viene presa di mira una stella, supposta all'infinito.
00:20 - Nell'arco di un giorno la Terra descrive un tratto dell'orbita attorno al Sole .
00:25 - L'effettivo periodo fisico di rotazione va riferito alla stella lontana (tempo siderale); per riallinearsi al Sole la Terra deve effettuare più di un angolo giro. La differenza è di circa un grado (quattro minuti - qui esagerato di un fattore 10).
00:34 - La stessa distinzione è immediatamente evidente per la Luna (la divisione è in giorni). Mentre la Luna ripassa dalla stessa fase (ad es. nuova), il sistema si sposta sulla sua orbita.
00:43 - Il periodo orbitale della Luna è da rifersirsi alle stelle (mese siderale) mentre il ciclo calendariale delle fasi è sensibilmente più lungo (mese sinodico - qui in scala).
Sia data una sfera elastica sottoposta ad una accelerazione gravitazionale.
0:05 - Se tale forza presenta un gradiente (qui è più intensa in basso), allora una parte dell'oggetto subisce una trazione maggiore di un'altra, ed il tutto si deforma proporzionalmente.
Una sfera elastica ideale assumerebbe quindi un profilo ellissoidale, sia trovandosi in caduta libera che in movimento orbitale (assimilare a una caduta continua).
0:15 - Nel caso della Terra, per brevità si considera la deformazione (molto esagerata) dell'idrosfera, ignorando quella atmosferica e quella, molto piccola, della massa solida.
Il primo agente responsabile delle maree è la Luna, considerata anch'essa rigida.
0:35 - L'ellissoide degli oceani e la presenza di una fase di alta marea nella direzione antilunare è dovuta anche ad una componente dinamica del sistema Terra-Luna: il suo movimento di insieme è imperniato sul baricentro (croce azzurra), che non corrisponde al centro della Terra.
0:40 - Poichè la Terra si muove in un mese attorno a questo punto, l'emisfero antilunare è soggetto ad una accelerazione centrifuga maggiore di quello sublunare (0:49).
1:00 - Il Sole interviene nel fenomeno in misura minore: benchè la sua attrazione sia maggiore, il suo gradiente è di gran lunga inferiore per via dei rapporti di distanza.
1:09 - Se la direzione delle forze è parallela, gli effetti si sommano (Luna piena e nuova).
1:14 - Se la direzione è perpendicolare, la deformazione è parzialmente compensata (Q = Luna ai quarti).
1:18 - Nel ciclo sinodico (fasi lunari) il fenomeno di marea viene quindi modulato da massimi (S = sigizie) e minimi (quadrature) periodici. Il grafico ne riporta l'intensità massima in condizioni geometriche semplificate.
1:54 – Si terrà ora conto della rotazione diurna della Terra (freccia gialla).
2:05 - Poichè la rotazione diurna è molto più rapida della rivoluzione sinodica, le fasi di marea vengono trascinate in anticipo rispetto al transito della Luna sul meridiano locale (freccia rossa). Lo sfasamento, qui accentuato, è di 3 gradi, e trasferisce momento angolare dalla Terra alla Luna, allungando i periodi (in origine la rotazione diurna era inferiore a 4-5 ore).
2:15 - Il grafico riproduce l'andamento semplificato di una marea diurna locale. Sulla Terra, le aree in rosso rappresentano i massimi e quelle blu i minimi. I periodi sono ora proporzionati.
2:30 - Si introducono gli elementi geometrici della rotazione diurna: coordinate, poli e piano dell'equatore terrestre e celeste.
2:40 - L'inclinazione della Terra rispetto alla direzione del Sole e all'orbita della Luna fa sì che i massimi e minimi di marea appaiano spostati periodicamente in latitudine, poichè la Luna e il Sole possono non avere la stessa altezza di culminazione in ogni luogo. Le aree colorate in rosso sono soggette al massimo sollevamento, quelle in blu al minimo.
3:20 - Osservando le medie latitudini in questa circostanza, è evidente che attorno al mezzogiorno (a sx.) l'alta marea è massima, ma all'opposto è meno marcata. Si vede come l’ampiezza possa variare quindi non solo con la latitudine, ma anche alla medesima latitudine secondo la fase dell’onda semidiurna.
3:58 – Con la Luna e il Sole sull’equatore si hanno le condizioni di massima simmetria del fenomeno.
4:30 – Il contrario, coi medesimi astri alle declinazioni più estreme.
NOTA - Il fenomeno reale risente in misura notevolissima di effetti dovuti a risonanze di oscillazione nei bacini, nonchè condizioni morfologiche e variabili meteorologiche specifiche, qui non considerate, ma assai diverse localmente.
"Ami del mar le amare maree?" (in memoria di Ciro Orefice, comandante).
L'aberrazione consiste in una deviazione delle posizioni stellari osservabile in specifiche direzioni. E' stata correttamente interpretata da Bradley come effetto di movimento dell'osservatore.
0:08 - Immaginando un cannocchiale in moto che punta una stella in direzione ortogonale, la luce in ingresso potrebbe (in caso estremo) non giungere all'oculare.
0:25 - Perchè la stella sia effettivamente vista al centro del campo, il cannocchiale dovrà essere ruotato di un certo angolo verso la direzione del suo movimento. Ciò non avrebbe luogo per un cannocchiale in quiete.
0:34 - L'angolo di deviazione dipende dal rapporto tra la velocità del cannocchiale e quella della luce. L'ampiezza massima misurata (circa 20 secondi d'arco, qui esagerata) indica che lo strumento si muove circa 10mila volte più lentamente della luce (C), ed è una delle prove del moto della Terra attorno al Sole (qui in km/sec). Questa misura viene indicata come Costante di Aberrazione.
0:48 - Schema di massima delle deviazioni apparenti delle stelle attorno alla propria posizione media, nel corso dell'anno. Come nel caso della parallasse annua, esse descrivono una traiettoria circolare quando sono situate sulla verticale del piano dell'eclittica, e con asse minore che si riduce a zero se viste sul medesimo piano (in blu equatore e coordinate equatoriali, in rosso l'eclittica).
1:58 - Il sistema di riferimento più adatto per questo come altri fenomeni planetari, è quindi quello eclitticale (in rosso).
NOTA - a differenza dll'effetto di parallasse, l'aberrazione interessa in egual misura tutti i corpi celesti indipendentemente dalla loro distanza, ed è sfasata rispetto a quella; inoltre la velocità della luce è invariante e quindi indifferente a moti propri stellari. L'illustrazione è geocentrica e non considera effetti locali di rotazione diurna, nè di lungo termine per il moto d'insieme del sistema solare.
Diagramma di Hertzsprung - Rosemberg - Russel (modificato Mogi).
Compare un campo celeste con un campionario di stelle di diversa luminosità e temperatura, tra le quali il Sole (crocetta).
0:04 - Nel diagramma (H-R in breve) compare in ordinate una scala di temperature (gradi Kelvin x 1000 in aumento verso sx.), e le stelle vengono ordinate secondo questo primo parametro, deducibile direttamente dal colore.
0:08 - Compaiono in ordinate la scala corrispondente all'indice di colore (blu - visibile) e le classi spettrali principali, corrispondenti alle temperature indicate.
0:13 - Compare in ascisse una scala di luminosità assoluta, deducibile da quella apparente tramite misure di distanza (parallasse), in termini di luminosità solare. Le stelle vengono nuovamente ordinate secondo quest'altro dato. In ascisse compare un'altra corrispondente scala di luminosità assoluta, in termini di magnitudine.
Si nota come la più parte delle stelle si collochi sul diagramma in modo non casuale: quelle più calde sono tipicamente più brillanti (sequenza principale). Sono indicate le eccezioni nelle loro più tipiche categorie; in particolare stelle che, pur non molto calde, appaiono ugualmente brillanti a causa delle grandi dimensioni (giganti), e altre che benchè molto calde brillano poco perchè piccole (nane).
0:36 - Il diagramma H-R viene riproiettato per inserire una terza dimensione ("H-R-M").
0:45 - Compare sulle nuove ordinate il terzo parametro di rilievo: la massa (in masse solari).
Questa può essere dedotta dopo i primi due parametri, dallo studio dei sistemi orbitali; le stelle vengono nuovamente riordinate in funzione di questo ultimo dato.
Si osserva una chiara relazione tra massa e luminosità: e soprattutto come una piccola variazione della prima comporti una notevolissima differenza della seconda (relazione alla terza-quarta potenza). Mentre i diametri delle stelle di sequenza principale sono molto simili, essi si diversificano enormemente per le nane e le giganti. Ugualmente estreme possono essere le densità e le luminosità; viceversa, è sempre assai limitata la gamma delle masse corrispondenti.
NOTA - gli oggetti riportati si riferiscono a stelle reali, sui cui parametri c'è accordo in letteratura. Il campione risente di un tipico effetto di selezione: le stelle di luminosità elevata paiono più numerose in quanto visibili anche a grande distanza, ma in effetti quelle intrinsecamente deboli sono molto più comuni, benchè più difficili da scovare. Si intuisce che in realtà il maggior numero si colloca al di sotto dei parametri del Sole, che non va considerato una stella "nana", ma una tipica gialla di sequenza principale.
Prende spunto dalla teoria cinetica dei gas, immaginando il caso ideale di un contenitore con due popolazioni riconoscibili di particelle differenti. Queste sono divise da un setto amovibile, supposte in equilibrio termodinamico e senza scambi con l'esterno.
0:16 - Togliendo il setto divisore, le particelle si diffondono liberamente e si giunge a una distribuzione omogenea col passare del tempo t. Si passa quindi da un ordine binario al momento t1 all'omogeneità di t2. L'entropia, manifestata come omogeneità, è aumentata, e questo può fornire una definizione di tempo coerente coi fenomeni osservati in natura. La sua direzione appare quindi univoca, non essendo noti fenomeni che possano spontaneamente portare ai casi da t2 a t1 in ordine inverso.
NOTA - fenomeni come le transizioni di fase (ad es. la cristallizzazione) possono apparire orientati nel senso di un ordine localmente crescente, ma in effetti ciò si verifica entro un sistema col quale scambiano energia, e quindi entropia.
La misura della circonferenza terrestre di Eratostene.
Il metodo si basa sulla diversa altezza del Sole in luoghi diversi.
0:17 - Il Sole sorge all'orizzonte di Alessandria e Assuan.
0:23 - Alla culminazione devia dallo zenith ad Alessandria, ma non dà ombra vicino ad Assuan (al tropico).
0:45 - Si suppone che la Terra sia sferica, e il Sole così distante che i suoi raggi siano paralleli.
0:55 - In tale caso, l'angolo della deviazione dalla verticale ad Alessandria è uguale alla differenza di latitudine fra le due località.
1:05 - Lo stesso rapporto si verifica fra la distanza meridiana dei due luoghi e l'intera circonferenza terrestre (circa 50:1).
NOTA - Il valore di 252.000 stadi è stato presumibilmente stabilito per convenienza di calcolo, in quanto numero divisibile per tutti i primi 10 numeri interi. La lunghezza dello stadio venne così riadattata nel III sec. A.C. quale sottomultiplo della circonferenza, come fu fatto nel 1799 per il metro.
Un pulsar (PSR) è una stella residuale, dalle caratteristiche fisiche estreme. Esito di un collasso gravitazionale, consiste di una massa stellare di neutroni e particelle esotiche ridotta a pochi km., e in rotazione velocissima per la conservazione del momento angolare. Caratteristica estrema è anche la densità del campo magnetico, che incanala correnti di particelle cariche accelerandole fino ai poli magnetici, dove producono un ampio spettro di radiazioni abbastanza collimate. Occasionalmente, tali macchie calde irradiano verso l'osservatore come un faro, producendo segnali periodici a tutte le lunghezze d'onda. L'esempio riproduce schematicamente l'emissione di un oggetto col suo periodo reale, con sovrimposto un campione audio del suo rumore radio.
NOTA - Scenario semplificato senza effetti relativistici, non più trascurabili per questo genere di oggetti.
I satelliti galileiani di Giove.
Osservazioni dei satelliti “medicei” di Giove, marzo 1613. Dalla sequenza riprodotta notte per notte, si è potuto dedurre il moto periodico di ciascuna luna (I – Io, II – Europa, III – Ganimede, IV – Callisto). Galileo riconobbe il significato del fenomeno quale evidenza di moti orbitali locali, e ne intuì il possibile interesse pratico quale metodo privilegiato di misura extraterrestre del tempo, svincolato dal nostro ciclo diurno.
Una possibile datazione astronomica delle piramidi del Regno Antico.
0:00 - Ci si posiziona a una latitudine media (non essendo molto rilevante il valore esatto dei siti). Le piramidi furono tradizionalmente allineate coi punti cardinali (cerimonia di "stesura della corda").
0:30 - Il Nord astronomico e geografico punta attualmente sulla stella Polare, ma il cielo viene riportato in precessione all'epoca media stimata.
0:40 - il polo N celeste medio dell'epoca era identificato con buona approssimazione dalla Alfa del Drago (Thuban), e su questo allineamento si presume che si identificasse il Nord, con l'Orsa Maggiore in culminazione superiore.
0:45 - Questo criterio è stato mantenuto per secoli, dunque si osserva una deviazione sistematica dal N (in primi d'arco, esagerata in pianta), essendo la piramide di Khufu (Cheope) quella meglio allineata, e quelle di Khafre (Chefren) e Shaure deviate in opposizione alla deriva dell'insieme.
1:04 - Si tiene ora conto del moto precessionale, che all'epoca era del tutto sconosciuto. Col passare dei secoli, l'allineamento stellare al Nord seguì quindi la deviazione dovuta al ciclo precessionale.
1:27 - Lo scostamento opposto delle piramidi di Khafre e Shaure si può riportare all'andamento d'insieme con un'operazione di simmetria. In tal modo, le fondazioni rientrerebbero nella scala cronologica comunemente accettata dagli archeologi.
1:38 - Per spiegare la caratteristica simmetrica dell'errore, si può ipotizzare semplicemente che tali allineamenti siano stati effettuati in corrispondenza della culminazione superiore dell'Orsa Minore anzichè quella Maggiore.
Se in tempi così lunghi non fosse intervenuto il movimento precessionale, non si sarebbe avuto alcun errore sistematico. Nè ciò si sarebbe verificato se il meridiano fosse stato determinato mediante la culminazione del Sole, procedimento più semplice ma che evidentemente non è stato seguito.
NOTA - L'ipotesi è di Kate Spence.
La caduta di un grave è influenzata dalla rotazione terrestre: considerazioni sul moto orbitale.
0:05 - Da un albero col tronco idealmente verticale cade una mela: la sua traiettoria è praticamente parallela al tronco. Si immagina quindi di aumentarne l'altezza fino a renderla confrontabile con le dimensioni della Terra.
0:25 - In una situazione statica, la traiettoria di caduta sarebbe ancora rettilinea, solo spostata ai piedi dell'albero per la convergenza al centro della Terra.
0:30 - Ora si tiene conto della rotazione terrestre (vista dal polo N). Le frecce bianche indicano il percorso della mela e del terreno nel medesimo intervallo di tempo.
0:37 - Durante la caduta la mela mantiene la componente trasversale del moto.
0:43 - Il punto di caduta si sposta necessariamente a precedere la verticale (ad est).
0:47 - Si aumenta ulteriormente l'altezza di caduta.
0:58 - La mela può avere una componente orizzontale sufficiente a deviarla completamente al di fuori della Terra.
1:05 - In tal caso entra in orbita.
Il moto orbitale periodico può essere considerato un caso di caduta infinita, tipicamente su traiettorie ellittiche. Ad una quota di 40mila chilometri, il periodo è geosincrono (pari alla rotazione terrestre); liberando la mela a questa altezza, essa non si discosterebbe dal punto di attacco.
NOTA - la traiettoria lunare ha un'ellitticità molto minore che non nel disegno.
Siano dati un emettitore e un ricevitore di onde, l’oscillatore E e il rilevatore R.
0:00 – In condizioni di quiete, il ricevitore R risuonerà con gli stessi parametri di frequenza e lunghezza d’onda coi quali è stata emessa.
0:22 – Se l’emettitore si muove, R rileverà un fenomeno modificato: accelerato in frequenza (minore lunghezza d’onda) in avvicinamento, il contrario in allontanamento. Si tratta dell’effetto Doppler, noto sia in meccanica che in elettromagnetismo.
0:45 – Nel caso in cui la velocità dell’emettitore sia maggiore di quella di propagazione del segnale, E lo può precedere, generando un fronte d’onda conico nella direzione di avanzamento. Nel campo delle onde acustiche è noto come effetto Mach, in quello elettromagnetico come effetto Cerenkov.
NOTA – Nessun emettitore può superare la velocità della luce C nel vuoto, ma il fatto si può verificare dove questa diminuisce in un mezzo otticamente denso (aria, acqua ecc).
Temperatura, volume e pressione
La relazione di queste tre grandezze nel caso di un gas ideale (legge di Boyle), senza transizioni di fase.
0:10 - In un contenitore chiuso da un pistone mobile a tenuta, un gas viene riscaldato. Mantenendo costante la pressione (peso P), si avrà un aumento di volume V (il pistone si alza per l'aumento della velocità cinetica delle particelle del gas).
0:23 - Per conservare il volume, all'aumento della temperatura si dovrà applicare una pressione maggiore (un peso P più grande).
0:38 - A parità di temperatura T, esercitando una pressione minore il gas occuperà un volume maggiore.
Miscellanea...
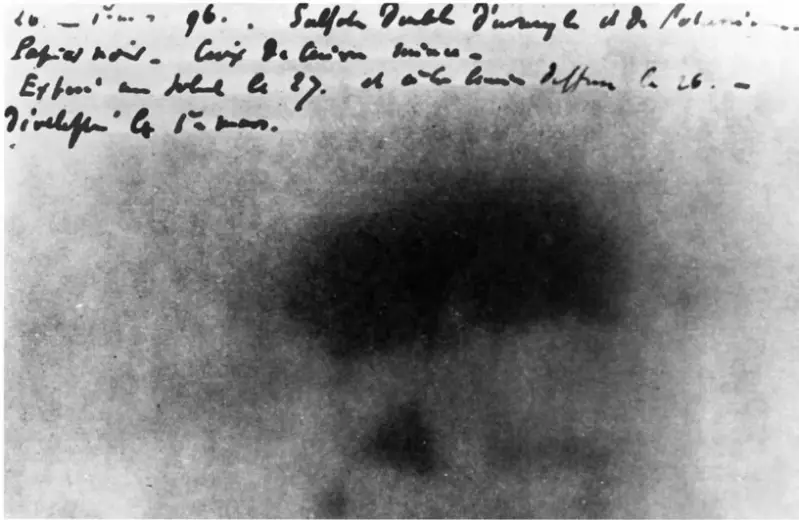
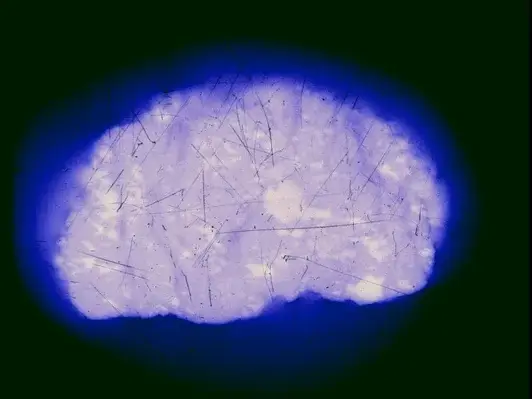
Autoradiografia: minerale d'Uranio su lastra fotografica
(Becquerel, 1896)
Autodiapositiva: Uraninite su pellicola invertibile
(Mogi, 1976)
"Honorable Mention" della National Science Foundation per video non-interattivi (2006):












































Crea il tuo sito web con Webador